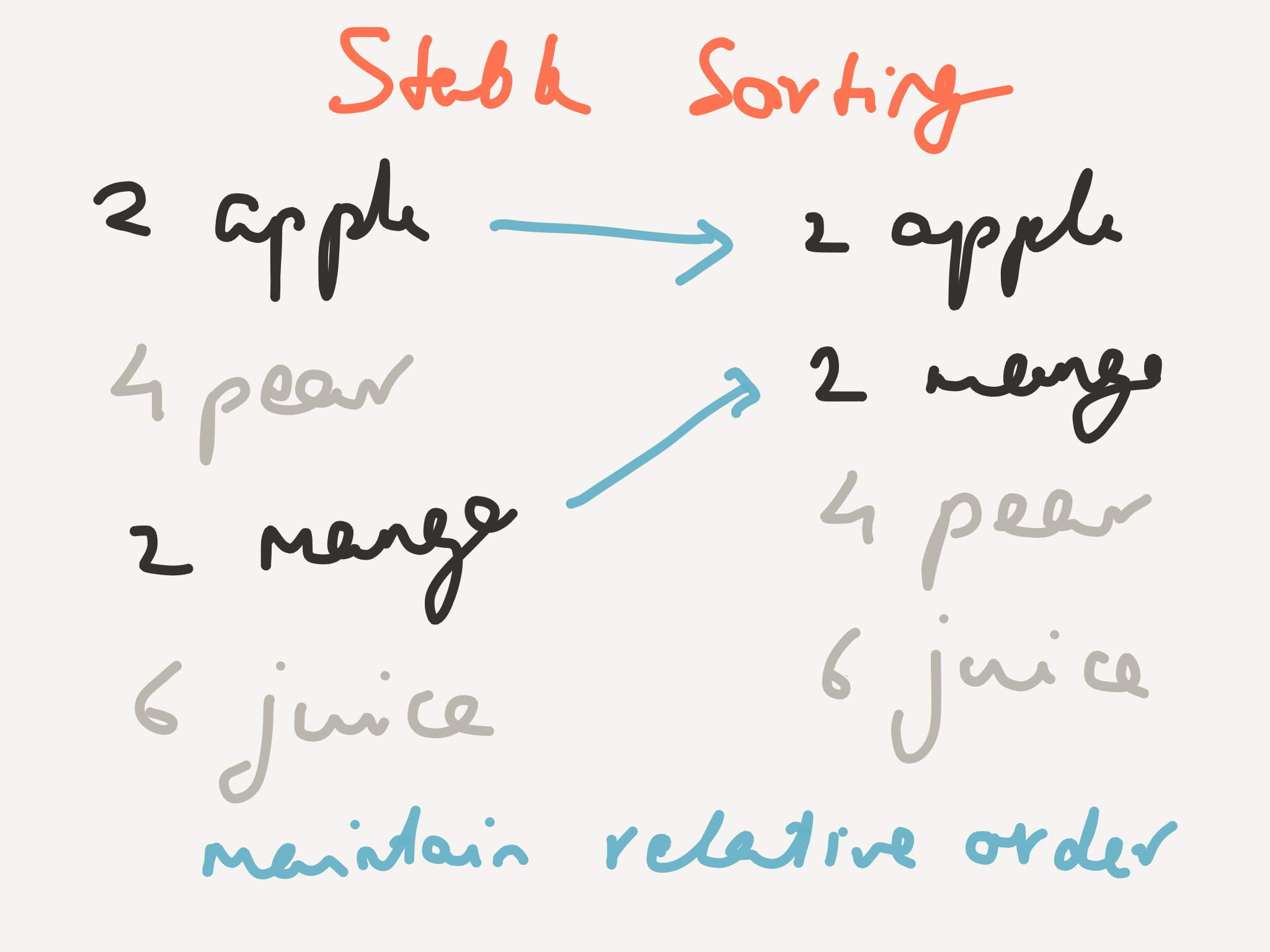
Stable sorting maintains the original order if two keys are the sameA sorting algorithm is stable if elements with the same value appear in the same order in the sorted list as they do in the original list.
Stable sorting maintains the original order if two keys are the same
For example, let’s say you have a class of students who have done a test. When grading them, you had their names in alphabetical order and you entered their score as you graded their answer papers.
Now you want to reorder the list so that it’s sorted by test score. What do you do when you have two (or more) students with the same score? A stable sorting algorithm would list them in alphabetical order (because that was the order in the original list).
Alicia 5 Christina 8
Bob 5 Erykah 8
Christina 8 -> Alicia 5
David 3 Bob 5
Erykah 8 David 3
Let’s look at an example of a stable sorting algorithm.
We’ll first set up a bucket for each possible grade. Then we’ll scan through our list of test scores, and if we see a 1 we’ll put it in bucket number 1, if the score is a 2 we’ll put it in bucket number 2, and so on until we’ve examined each score. We’ll also make sure the first item that goes in to a bucket is the first one out.
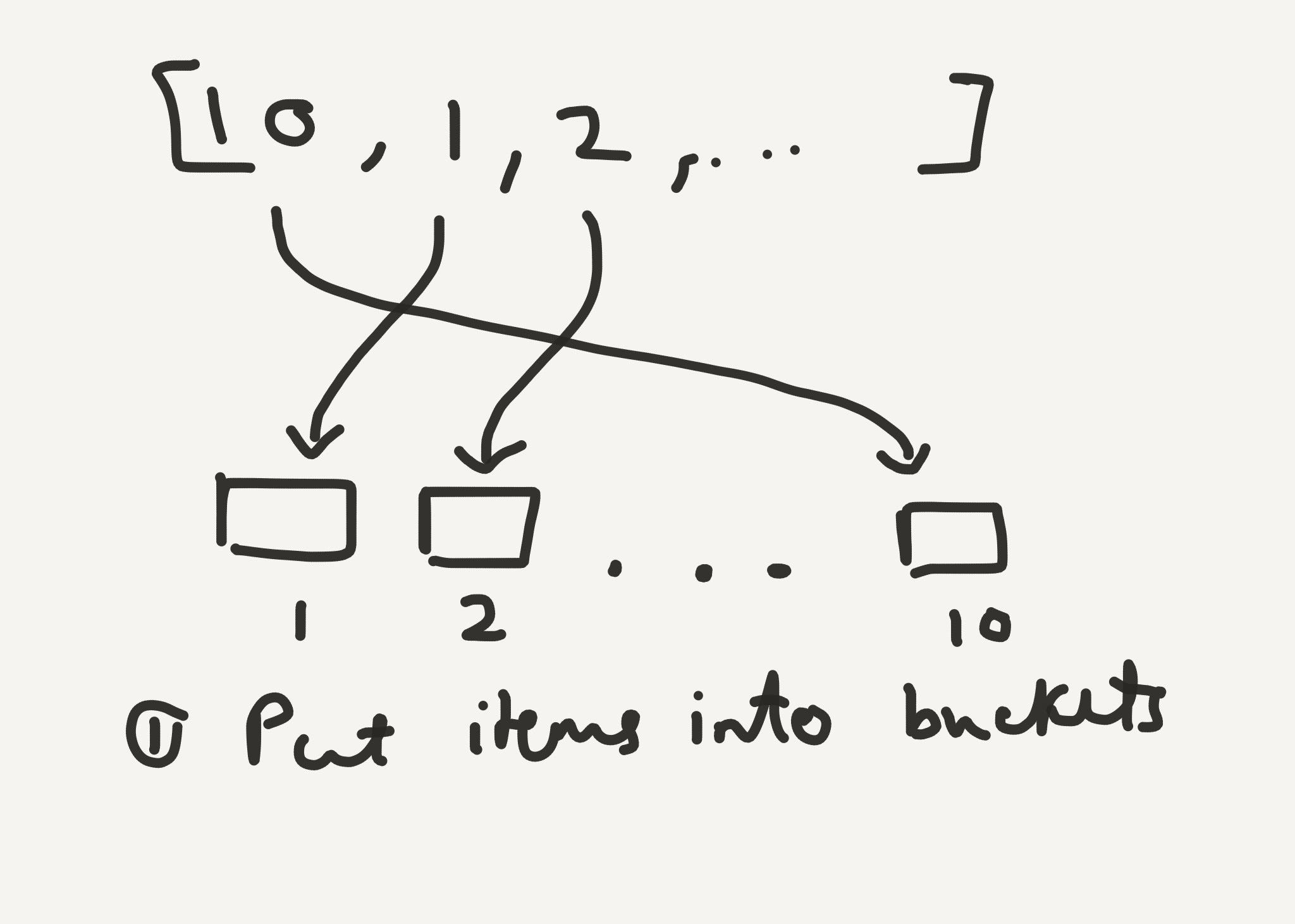Step 1 for Bucket Sort
Now to sort the results, we’ll first empty bucket number 10, then empty bucket number 9 and so on until we empty the last bucket.
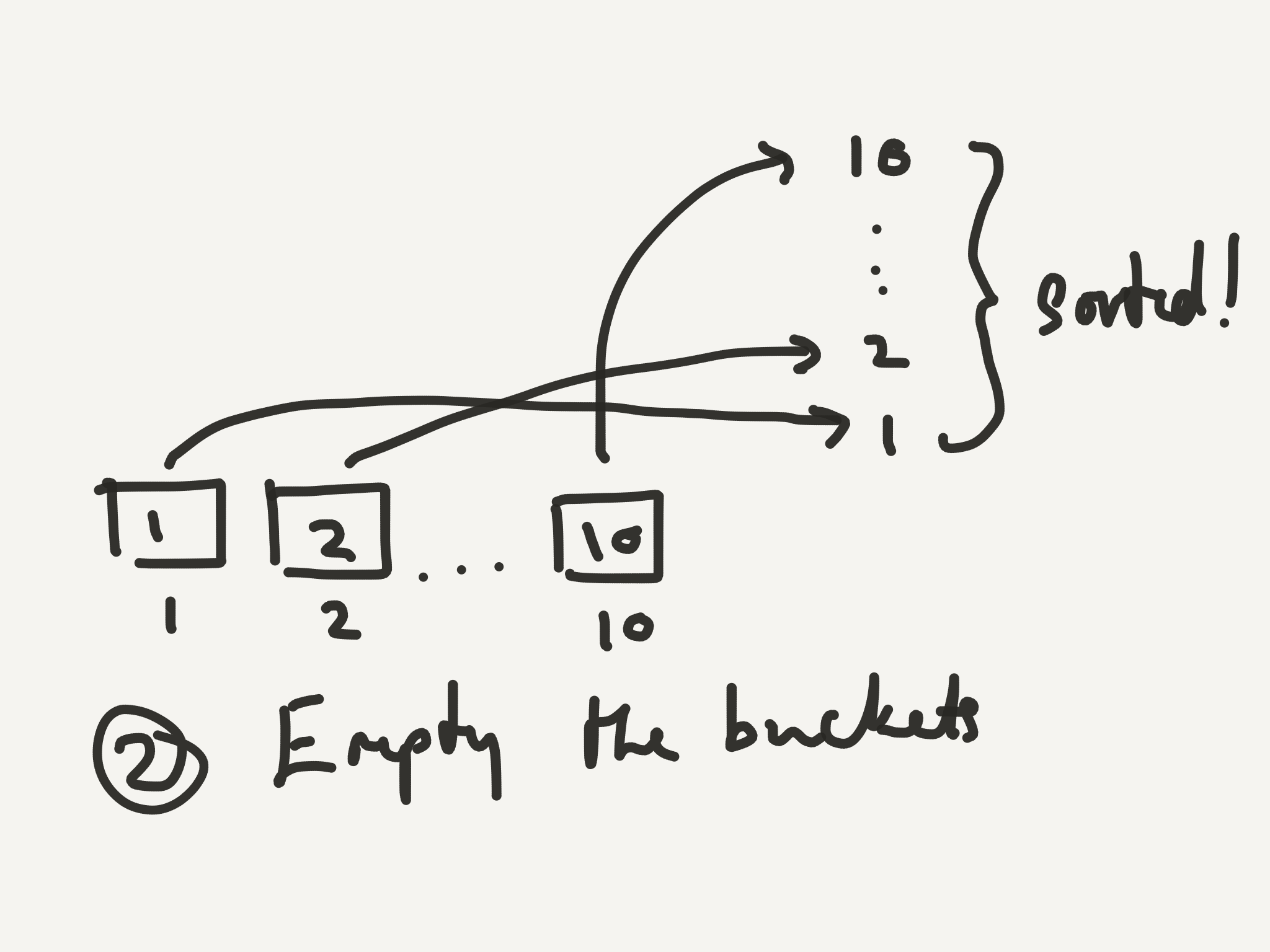Step 2 for Bucket Sort
If there is more than one item in a bucket, we know that the first item that was put in will be the first one out. This means the order of the original list is preserved within each score.
In Python, this would be:
def bucket_sort(items_with_keys):
"""Takes a list of keys and items,
and performs a stable sort - if there are two
items with the same key, they are in the same
order in the sorted list as in the original list"""
buckets = [[] for n in range(0, 10)]
sorted_items = []
for (key, item) in items_with_keys:
buckets[key].append(item)
for bucket in buckets:
sorted_items.extend(bucket)
return sorted_items
Why is this cool? I’m glad you asked!
Let’s say you’re now sorting items that range from 1 to a million. It would be a pain to keep track of a million buckets. Let’s stick with our 10 buckets (er… now they’re labeled 0, 1, … 9). Let’s also make the range 1 to 9999 so that my examples are easier to type out 😅 Finally, let’s sort them in ascending order this time 😆
We could first sort by the first digit in the number, then sort by the second digit, then by the third, and so on until we reach the end of the number. This is pretty much how you might think about years — you know that everything that happened in the 19th century happened before anything in the 20th century, and anything in 1950 happened before anything in the 90s, and so on.
9999 0001 0001
0001 0100 0099
0100 -> 0099 -> 0100
1000 1000 1000
0099 9999 9999
That idea was easy to describe, but it sounds like a pain to actually implement — you have to make buckets within the zero bucket to sort the items that start with a zero, etc.
So let’s skip ahead and go straight to radix sort.
The idea behind radix sort is to sort the numbers from the least significant digit onwards to the most significant. This has the disadvantage of being counter-intuitive, but the very real advantage of being straightforward to implement! Once again, we’ll use the stable sorting algorithm we described earlier, and hopefully the reasons will be clear soon.
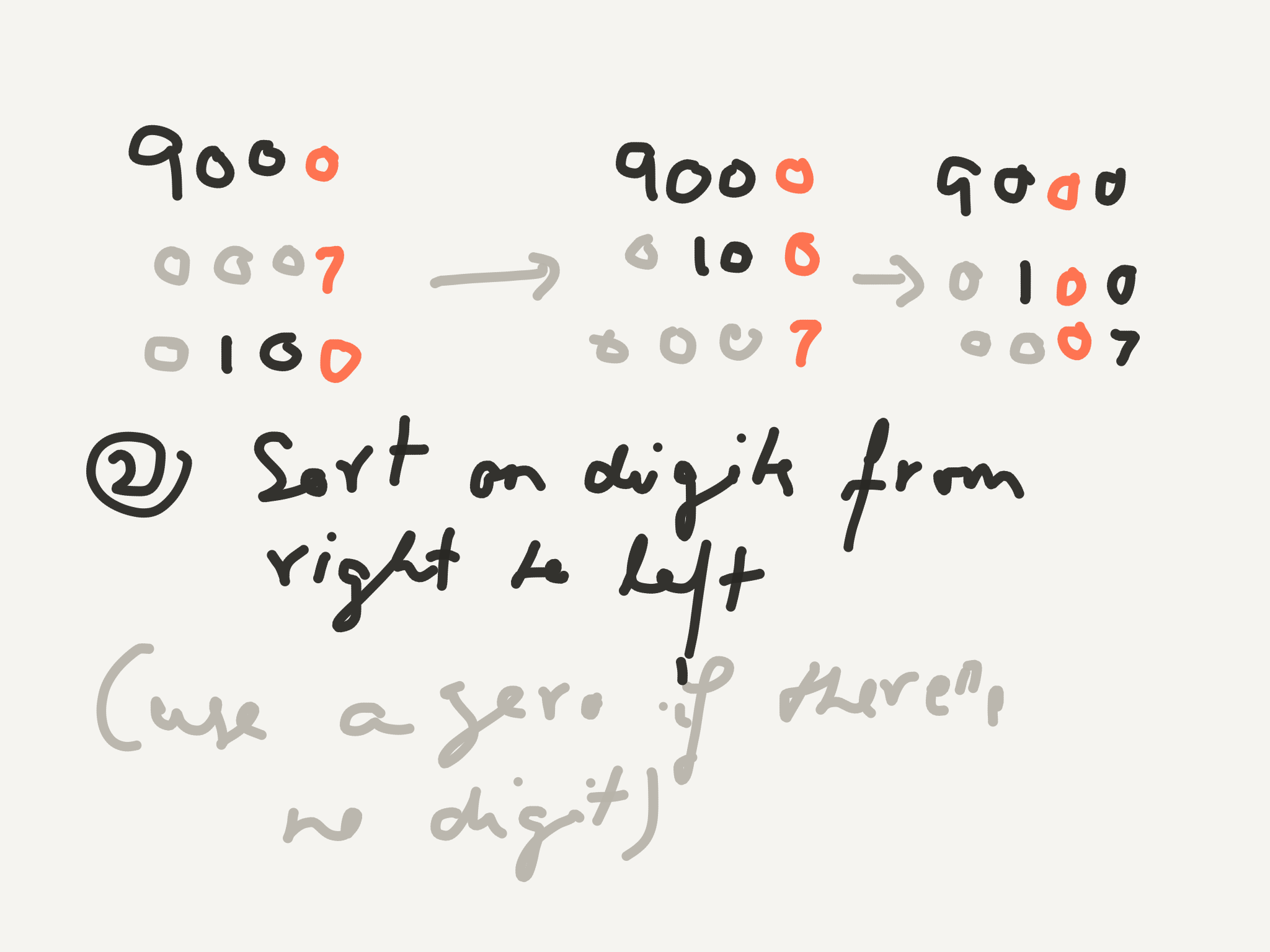
Note that we can use leading zeroes to help sort 7 and 1000 on digit 3!
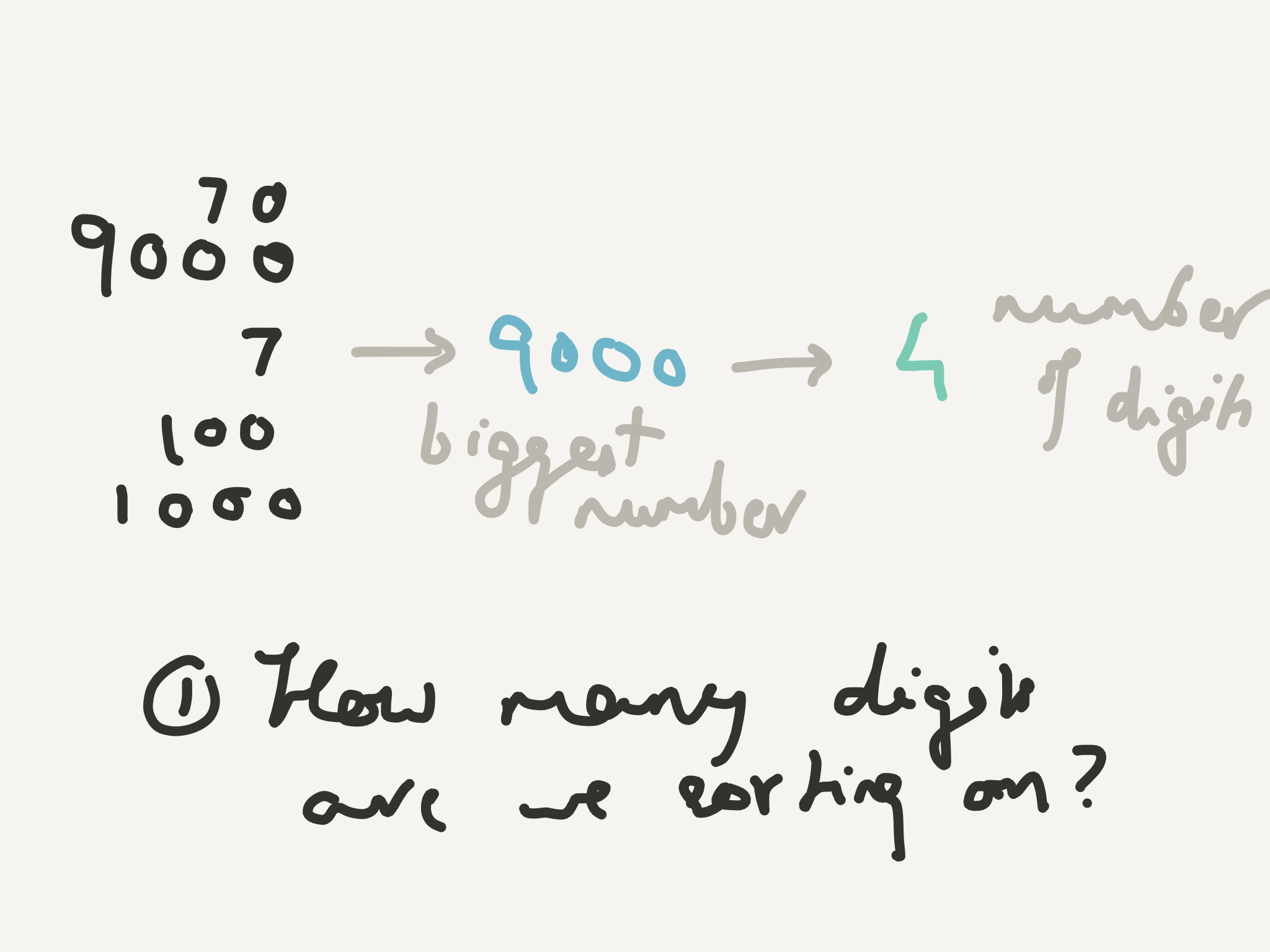The first step in Radix Sort is to make sure we have digits to sort on 😃
Perhaps an example would be good here!
9999 999**0 **10**0**0 1**0**00 **0**099
9990 100**0** 02**0**0 0**0**99 **0**100
1000 020**0 **01**0**0 0**1**00 **0**200
0200 -> 010**0** -> 99**9**0 -> 0**2**00 -> **1**000
0100 999**9 **99**9**9 9**9**90 **9**990
0099 009**9 **00**9**9 9**9**99 **9**999
We’ve first sorted on the smallest digit in the number (on the right) and then the second smallest, and so on till we reach the left-most digit.
Starting with the right most digit, sort the numbers using a stable sorting algorithm
The individual steps don’t make much sense, but it’s helpful to notice two things:
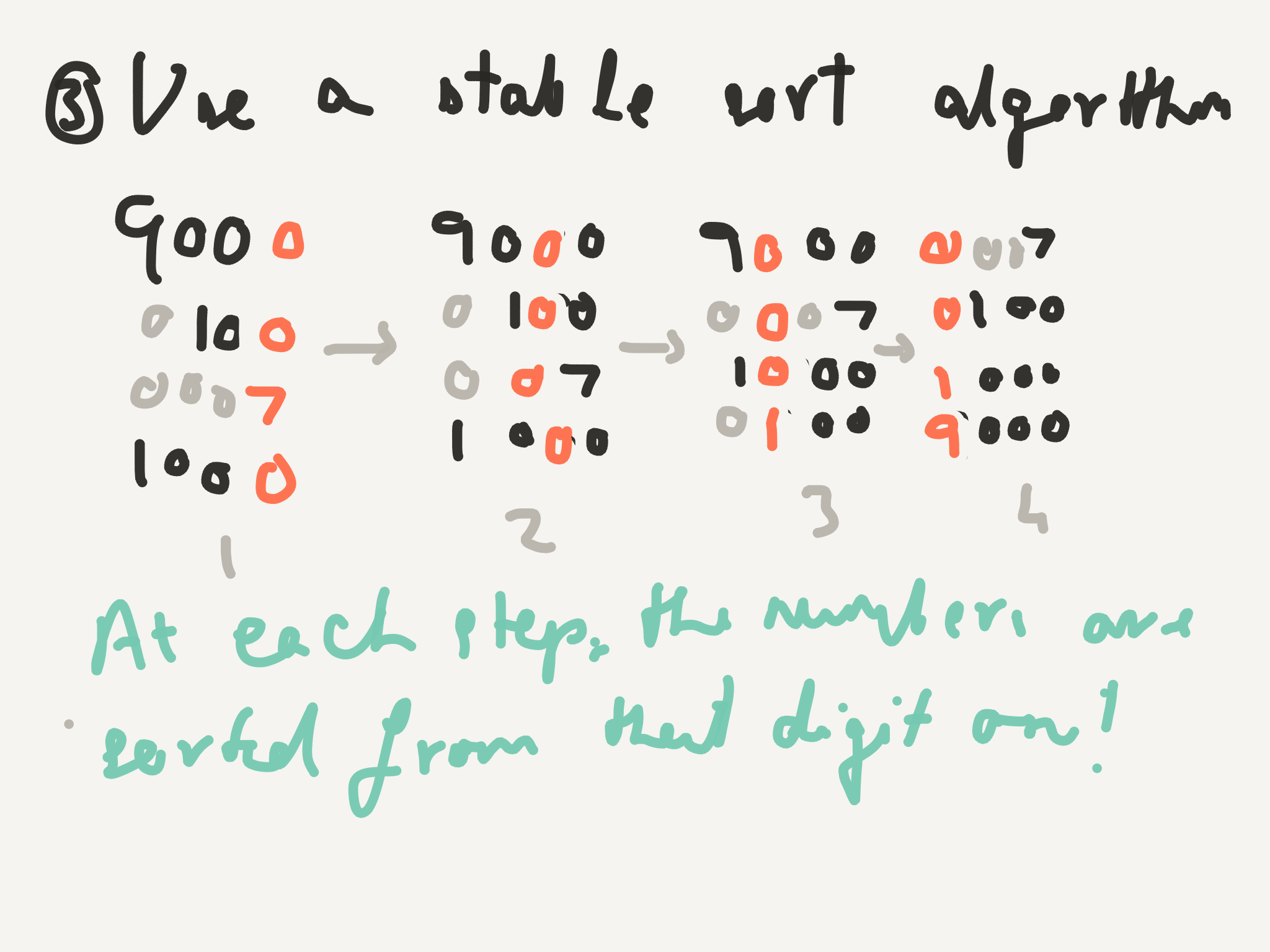At the last step, the numbers are sorted on all the digits!
So if there are two numbers with the same first digit (e.g. 0007 and 0100) by the second observation, since they have the same first digit, they are in the order in which they were in the previous step. Which is the order in which the second digit is sorted.
But wait, you say, is this really easy to implement? Yes!
def get_digit_number_tuples(digit, numbers):
"""Make a (digit value, number) tuple for bucket sort"""
return [(get_digit(digit, n), n) for n in numbers]
def get_max_digits(numbers):
"""Figure out how many leading 0's the numbers need
to be padded with"""
return len(str(max(numbers)))
def radix_sort(numbers):
"""Sort from the least significant digit to
the most significant digit"""
for d in range(0, get_max_digits(numbers)):
numbers_with_digits = get_digit_number_tuples(d, numbers)
numbers = bucket_sort(numbers_with_digits)
return numbers
Radix sort is like four lines of code! Note that get_digit() is from this stack overflow answer, modified to handle 0099 😃
def get_digit(digit, number):
# ** is integer pow()
# // is integer division
if number < 10 ** digit:
return 0
return number // 10**n % 10
Note that this sorting algorithm is linear (if the number of digits can be treated as a constant) 🎉
Thanks to Nathan Weeks Shane and Julian Squires for their feedback and suggestions — one of the many joys of the Recurse Center!
I’m looking for summer internships for next year, get in touch if you’re hiring!
